척척석사가 되어보자
활성화 함수(Activation function) 본문
혼자끄적이는 공부
활성화 함수가 "입력값과 가중치(weight)의 곱의 합"의 강도를 조절해 주는 것은 알겠지만 어떠한 상황에서 적절한 활성화 함수가 무엇이고 어떤 장단점이 있는지 잘 몰라서 정리를 해보았다.
공부하면서 느낀건데 이 활성화 함수들의 장단점을 정확히 이해하기 위해 순방향(feeforward)과 역전파(back propagation) 계산을 직접 해보아야 겠다는 생각을 하였다. 그래야 Vanishing gradient 문제를 이해할 수 있을것 같다. 다음 포스팅은 역전파 계산과정을 써보아야겠다.
1. sigmoid 함수

보통 1 또는 0의 활성함수 값을 갖는다.
장점 : 선형 관계가 아니다 ( 선형모델에서는 종속변수에 대한 비례가 100%가 넘어갈수 있어 이치에 맞지 않는다. 예를들어, y=0.01x+0.01 일때 x가 100이면 y는 1.1이되어 110%가 된다.)
단점 : 신경망이 깊어지면 역전파(back propagation)을 하는 과정에서 입력값이 작으면 미분값이 0에 가까워 지기 때문에 의미를 잃어간다. 또 입력값이 커지면 미분 값이 1에 수렴하기 때문에 가중치 값이 거의 변하지 않는다.(이 사실이 명확히 와닿는지 않는다. 나중에 역전파계산을 해보아야겠다.) 이 문제를 Vanishing Gradient라고 한다.
2. tanh
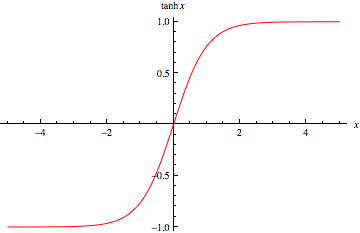
sigmoid와 다르게 -1부터 1까지의 값을 갖는다.
장점 : sigmoid에서는 중점이 0.5였는데 여기서는 0이다. (중점이 0.5이면 입력값에 대한 가중치 값을 판단하기 어려워 진다 한다. 이것도 나중에 계산해보자)
단점 : sigmoid와 같다.
3. ReLu ( Recticified Linear Unit)

장점 : 연산중 exponential과정이 없어 계산이 빠르다. Vanishing Gradient 문제가 해결된다.
단점 : 0보다 작으면 결과가 0이기 때문에 몇몇 노드들이 죽는 현상이 일어난다. ( Lelu에서 입력이 0이상일때 미분하면 상수만 남는데 이것도 그럼 입력값에 대한 가중치 값을 반영을 못하는것 아닌가 ? 선형 모델에서의 문제점과 다를게 뭐지 .. 이것도 계산해보아야겠다)
결론적으로 상황에 따라 맞는 활성화 함수가 존재한다.
'머신러닝 > 개념공부' 카테고리의 다른 글
| logistic regression 개념 복습 (0) | 2018.10.12 |
|---|---|
| linear regression 개념 정리 (0) | 2018.09.11 |
| 0. Supervised Learning (0) | 2018.09.04 |


